ATS Design (Day-to-day version)
At the beginning of a day random travelers are generated from the origins, and the commuters estimate the travel time and/or choose the shortest route based on experiences. The commuters depart along the chosen shortest route according to their predictions. A required arrival time is set as the reference time, and the commuters are required to arrive at the destination before the time. The commuters will not be punished because of lateness. At the end of a day all travelers will be cleared in order to make traffic conditions of all day are similar.Contents
Setting
Travelers
Prediction of Travel Time on No Experience Links
Origin and Destinations
Traffic Signals Setting-up
Outputs
Home
SETTING
-----------------------------------------------------------------------------
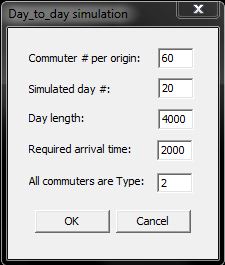
Commuter # per origin -- the number of commuters adhering to an origin; Setting it as ZERO makes the day-to-day version be the regular one.
Simulated day # -- the total number of simulated days;
Day length -- the number of simulation steps in a day;
Required arrival time -- commuters are required to arrive at their destinations at the time;
All commuters are Type -- the type of commuters in this trial (Refer to Types of Commuters).
Top
TRAVELERS
-----------------------------------------------------------------------------
There are two types of travelers currently:
Random travelers. We call the travelers travel only once from the generation origin to a random destination as random travelers. We generate random travelers by a binomial distribution.
Commuters. We classify commuters into three types by experience accumulation and changing route or not. The commuters in Type-1 and 2 choose routes based on the average of past experiences, while the commuters in Type-3 based on the experience of last time. Type-1 commuters always travel along the distance shortest route and only change the departure time based on the experience. They are kind of habit commuters that are quite common in real life. In addition, we assume the commuters depart the origin strictly following the predicted travel time; i.e., the departure time equals to the required arrival time minus the predicted travel time. The three types are presented as follows
Experience accumulation |
Changing routes |
|||
Average |
Last time |
Yes |
No |
|
Type-1 |
T |
T |
||
Type-2 |
T |
T |
||
Type-3 |
T |
T |
||
Top
PREDICTION OF TRAVEL TIME ON NO EXPERIENCE LINKS
-----------------------------------------------------------------------------
We assume all travelers know the network and estimate the travel time Tp on the no experience links by the three components: (1) Free-flow travel time Tf, the travel time that vehicle run with the maximum (limited) speed u; i.e., Tf=L/u where L is link length; (2) Waiting time in front of traffic lights Tw, the waiting time because of the red light in front of intersections; (3) Estimation errors e, the errors are arising from humaní»s irrationality. We assume that
Tp=(Tf+Tw)e If travelers arrive at the intersection as the same probability, then
Tw=(1+...+Tr)/Tr=(1+Tr)/2 where Tr is the average red light time. We also consider errors e be in [-1,1] to match the multiply in the function of Tp. Considering the estimation errors are not only to reflect human's irrationality, it also can avoid the weakness of Dijkstra's algorithm. The algorithm only gives us one and always the same one shortest route when routes with the same shortest distance exist. Therefore, we prevent the overload of links because of shortest routes are ignored.
Top
ORIGIN AND DESTINATIONS
-----------------------------------------------------------------------------
All links between two intersections have an origin and a destination located in the middle of links. Only a destination is available in the links connecting exits and intersections and locates at the end of the links. Likewise, only origin is available in the links connecting entrances and intersections and locates at the beginning of the links. Additionally, Dijkstra's algorithm is employed to calculate the shortest route between an origin and a destination.
Top
TRAFFIC SIGNAL SETTING-UP
-----------------------------------------------------------------------------
All intersections have a fixed two-phase fixed-cycle traffic signal with the same cycle length 100s and the same green and red-amber time 50s. The traffic light offsets are randomly selected from a uniform distribution with parameters 0 and 50s. The right turn is not controlled.
Note: This is a default setting with provided XML file. One can change the setting by the XML file.
Top
OUTPUTS
-----------------------------------------------------------------------------
A fold named "OutputData" will be created after the program is run. The output files are
Setting.txt
The basic setting of this trial.
MFD.csv
Column 1: average flow
Column 2: average density
DepartureArrivalRate.csv
The departure and arrival number of travelers at each time slice.
Column 1: Commuter Arrival number
Column 2: Random Traveler Arrival number
Column 3: Commuter Departure number
Column 4: Random Traveler Departure number
DepartureTime(Commuter1080).csv
In the simulation model, we can track some commuters (One have to set it in the codes -- SimuFun::Set_Commuter_On_Origin, however)
Departure time of each day
RouteChoice(Commuter1080).csv
In the simulation model, we can track some commuters (One have to set it in the codes -- SimuFun::Set_Commuter_On_Origin, however)
The first row is the commuter's predictions of the travel time on each link of the network
Other rows are the actual travel time. Note that the travel time that are different from the first row is the chosen one, otherwise it is not chosen in this day.
SpatialDistribution.csv
Comulmn 1: Day number
Comulmn 2: Time slice (currently, every 300sec we record the data once.)
Rows: Corresponding to 142 links
Contents: Vehicle number on the link at the time
Top